-

-
因子分析模型
來源:默認管理員點擊數:558發布時間:2012-12-101 基本概念:在市場研究中,由于多種因素的影響,指標間往往具有較大的相關性。如:在香煙口味測試中,“刺激程度”與“勁頭”之間、“口感”與“香氣”之間存在線性相關關系,考核“刺激程度”對“總體滿意度”的影響必須考慮來自“勁頭”的間接作用;又如:在房地產市場研究中,樓盤評估指標體系“穩重的、守信用的、尊貴的、前衛的、…”之間相關性比較大,給分析帶來一定的困難,需要進行指標的二次設計,既需要從中抽取出具有代表性、獨立的指標。
因子分析(Factor Analysis)是解決上述問題的有效方法之一,它通過對原始指標體系內部相關性、結構的研究,借助特定的統計技術,將原始指標轉化為與之信息等價的、獨立的新指標,既因子(Factors),通過對因子的研究,達到對事物本質認識的目的。
2 基本原理
設原始指標向量為X=(X1,X2,…,Xn),各變量的均數、標準差、標準化變量分別為 、Si、xi(i=1,2,…,n),相互間的關系為:
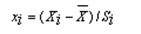
以R表示相關系數矩陣,理論可以證明,存在正交標準化變量f=(f1,f2,…,fn)、正交矩陣L=(lij)n´n,使得

將方程展開,表達式為:
f1=b11x1+b12x2+b13x3+……+b1nxn
f2=b21x1+b22x2+b23x3+……+b2nxn
……
fn=bn1x1+bn2x2+bn3x3+……+bnnxn
也可以寫成:
x1=b11f1+b21f2+b31f3+……+bn1fn
x2=b12f1+b22f2+b32f3+……+bn2fn
……
xn=b1nf1+b2nf2+b3nf3+……+bnnfn
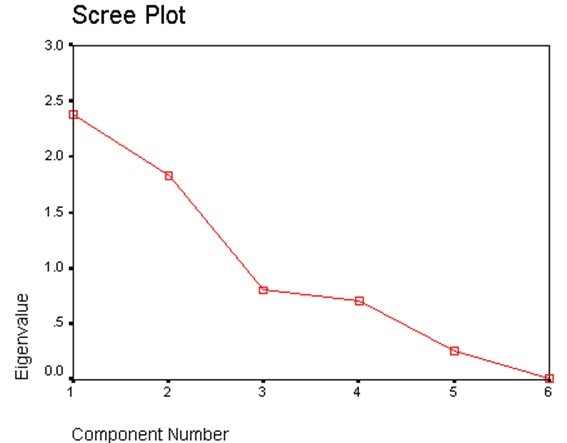
我們稱f1、f2、…為第一公因子、第二公因子、…。li(i=1,2,…,n)表示相關矩陣R的特征根,等于相應公因子的方差(并且有l1³l2³…³ln),表示該公因子對數據的解釋能力,常稱之為該公因子的貢獻(Contribution), li/n稱之為該公因子的貢獻率(Contributions rate)。實際工作中,常以累計貢獻率決定選取公因子的多少,一般來說,累計貢獻率達到85%即可。
因子分析示例:
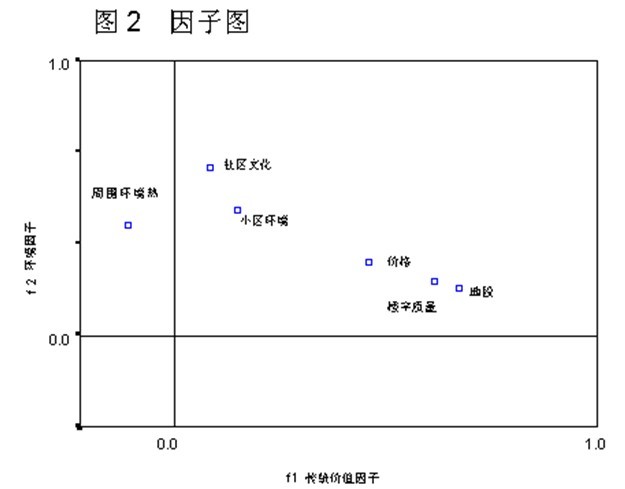
一項針對消費者購房影響因素研究中,經過因子分析,提取了前2個公因子,分別為:
f1=0.98地段+0.93樓宇質量+0.81價格+0.15小區環境+0.10社區文化-0.23周圍環境
f1=0.15地段+0.20樓宇質量+0.35價格+0.80小區環境+0.85社區文化+0.63周圍環境
從方程中我們可以歸納出:第1因子主要由“地段、質量、價格”決定,所以我們可以稱之為“傳統價值因子”;第2個因子主要由“小區環境、社區文化、周圍環境”決定,均與環境密切相關,因此我們稱之為“環境因子”,相應碎石圖為:
第一、二公因子定位圖為:
上一篇下一篇