欧美性欲视频_国产一区正在_91久久精品国产91性色tv_精品动漫3D一区二区三区免费版_91精品久久久久久久_久久天天操

　　主要內容：

　　l樣本容量確定的方法

　　l 正態分布及其評價

　　l理解總體、樣本和抽樣分布

　　l點估計與區間估計

　　l 抽樣平均數和抽樣比例

　　5.1 確定概率抽樣的樣本量

　　在確定概率抽樣樣本容量的過程中會遇到涉及財務、統計和管理三個方面的問題。一般原則是，樣本越大，抽樣誤差就越小。但樣本大，耗費的成本也高，而且一個項目可支配資源畢竟是有限的。雖然抽樣成本隨著樣本容量的增加呈直線遞樣(樣本容量增加1倍，成本也增加1倍)。抽樣誤差卻只是以樣本量相對增長速度的平方根遞減。即如果樣本量增加了3倍，數據搜集成本也增加了3倍，而抽樣誤差只降低了1/2。最后一點，樣本容量計算還反映了管理方法的問題。要求多高的估計精確度?實際總體值在所選定的置信區間內的置信度是多少?正如你將在本章中學到的，有許多種可能性。有的情況要求精確度較高(抽樣誤差很小)，并且要求總體值在較小誤差范圍以內的置信度較高。而有些情況則不要求這些。

　　5.2 確定樣本容量的方法

　　5.2.1 可支配預算

　　某一研究對象的樣本容量通常直接或間接地由可支配的預算額所決定。因此，順序上，樣本容量通常是稍后才確定的。一個品牌經理如果有40000美元預算可用于某項市場研究，那么除去其他項目成本(如調查方案和問卷的設計、數據的處理、分析等)后，余下的那部分預算才決定著被調查的樣本容量的大小。如果可支配資金太少，可以確定的樣本量太小，就必須做出決策，是補充更多的資金還是放棄這一項目。

　　雖然這種方法看來缺乏科學性和過于武斷，但是在一個離不開財務資源預算編制的整體環境下它確實存在。財務上的限制要求調查人員的設計方案要利用有限的資源提供有利于決策的高品質的數據資料。“可支配預算”方法使調研人員不得不尋求多種選擇的搜集方法并謹慎衡量信息的價值及其成本。

　　5.2.2 單憑經驗的做法

　　一些客戶會指定REPs(對計劃的具體要求)，他們會要求樣本容量為200、400、500或其他的特定量。這個數據的確定有時是出于對抽樣誤差的考慮，而有時則只是依據以往的經驗和過去進行的相似調研中采用的樣本量。對指定樣本容量這種做法的全理解釋歸結起來只能說是“一種強烈的感覺”，認為某一特定的樣本容量是必要的或適當的。

　　也許有人認為客戶指定的樣本容量有利于計劃調研目標的實現。有些情況下，調研人員會認為指定的樣本容量不符合要求。這時，調研人員有職責向客戶提出擴大樣本容量的建議并讓客戶做出最后的決定。如果擴大樣三容量的建議遭到了否決，調研人員會拒絕提交計劃，因為他(她)認為樣本容量不合要求會嚴重影響調研成果。

　　5.2.3 要分析的子群數

　　在任何確定樣本容量的問題中，都必須認真考慮所要分析并要據此做統計推斷的總體樣本的各個子群的數目的預期容量。例如，從整體上看樣本容量為400很符合要求，但若要分別分析男性和女性被調查者，并且要求男性與女性的樣本各占一半，那么每個子群的容量僅為200。這個數字是否符合要求，能使分析人員對兩組的特征做出預期的統計推斷呢?再如，要按年齡和性別分析調研結果，問題就變得更復雜了。假設要按以下方式將總體樣本劃分為四組：

　　l 35歲以下的男性

　　l35歲以上的男性

　　l35歲以下的女性

　　l 35歲以上的女性

　　如果預計每組約占總樣本的25%，那么子群容量僅有100。 這個數字能否使我們按照調研目標的要求對各組分別做出統計推斷呢?隨著樣本量的縮小，抽樣誤差的增加，會出現這樣一個問題，那就是調查人員很難辨別依據現象所得的兩組間的差別(如表明打算購買新產品的百分比)是真正意義上的差別還只是由抽樣誤差引起的差別。

　　在其他條件相同的情況下，所要分析的子群數目越大，所需的總樣本容量也就越大。一般認為樣本量要足夠大，以便每個主子群的容量至少為100，而每個次子群的容量至少也有20-50。

　　5.2.4 傳統的統計方法

　　你可能在其他書上見過確定簡單隨機樣本的傳統方法。回顧一下這些方法。在利用抽樣結果做重要推斷時需要三條信息：

　　• 總體標準差的估計值

　　• 抽樣的允許誤差范圍

　　• 抽樣結果在實際總體值的特定范圍(抽樣結果±抽樣誤差)內的預期置信度。

　　有了以上三條，就可以計算出簡單隨機抽樣所需的樣本容量了。

　　5.3 正態分布

　　5.3.1 總體特征

　　在古典統計推斷中，正態分布居于特別重要的地位。這有以下幾面原因：首先，市場人員遇到的許多變量其概率分布都趨于正態分布。如，軟飲料包裝的數量;愛吃快餐的人平均每月吃快餐的次數;每星期看電視的平均小時數。其次，有理論上的原因。比較重要的一條是大數定理、中心極限定理。根據該定理，對于任何總體，不論其分布如何，隨著樣本容量的增加，其抽樣平均數的分布趨于正態分布。這種趨向的重要性將在后面做詳細說明。再次，許多離散型概率的分布也近似于正態分布。例如，將大量的某地男性身高值標在一張圖表上，就會得到如圖5-1的分布圖，這種分布就是正態分布，它有以下幾個重要的特征：

　　(1) 正態分布呈現鐘形且只有一個眾數。眾數代表著集中的趨勢，是發生頻率最高的那個特殊值。兩峰的(兩個眾數)分布有兩個峰值;

　　(2) 正態分布關于其平均對稱。也就是說它是對稱的。它集中趨勢的三個衡量標準(平均數、中位數和眾數)是相等的。

　　(3) 一個正態分布的特殊性由其平均數和標準差決定。

　　(4) 正態曲線下方面積等于1，表明它包括了所有的調查結果。

　　(5) 正態曲線下方在任意兩個變量值之間的面積，等于在這一范圍內隨機抽取一個觀察對象的概率。以圖5.1為例，一次抽取到一名男性，其身高在172cm-177cm之間的概率為34.13%。

　　(6) 正態分布還有一個特點，就是所有的正態分布在平均數±1個標準差之間的面積相同，都占曲線下方面積的68.26%或者說是占全部調查總體結果的68.26%。這叫做正態分布的比例性，這一特點為本章將要計論的統計推斷提供了基礎。

　　5.3.2 標準正態分布

　　任何正態分布都可以轉換為標準正態分布。標準正態分布的特點與正態分布相同。只有標準正態分布的平均值等于0，標準差等于1。正態分布的任何一變量值X通過一個簡單的轉化公式就能變換成相應標準正態分布中的Z值。這種轉換是由正態分布的比例性決定的。用符號表示：

　　用符號表示：

　　式中X——變量值;

　　μ——變量平均值;

　　σ——變量標準差。

　　圖5.2 標準正態分布圖

　　變量Z的標準正態分布曲線下各塊面積(全部百分比)都列在表5.1中。

　　表5.1 Z值為1，2，3時標準正態曲線下方的面積

　　5.4 總體分布、樣本分布和抽樣分布

　　進行抽樣調查，目的是要對總體做出推斷，而不是為了描述樣本的特征。總體，就像前面定義的，包括可以從中獲取信息達到調研目標的全部可能的人體或物體。樣本是總體的子集。

　　總體分布是總體中所有單位的頻率分布。這一頻率分布的平均數，通常用希臘字母μ表示，標準差用希臘字母σ表示。樣本分布是單個樣本中所有單位的頻率分布。樣本分布的平均數常用 表示，標準差用S表示。

　　在這里，有必要介紹一下三種分布，樣本平均數的抽樣分布。理解這一分布對于充分認識估計簡單隨機抽樣誤差的依據十分重要。樣本平均數的抽樣分布是指從一個總體中抽取一定數量的樣本，由樣本平均數構成的概率分布。雖然人們對很少計算這種分布，但它的特性具有很大的實際意義。要獲得樣本平均數的分布，首先要從特定總體中抽取一定量的樣本(如25000)，接著，計算各樣本的平均數，并排列出頻率分布。因為每個樣本由樣本單位的不同子集構成，因此樣本平均數不會完全相同。

　　當樣本的單位數和隨機性足夠大，樣本平均數的分布近似于正態分布。這一論斷的基礎是中心極限定理。該定理說明，隨著樣本容量的增加，從任一總體中抽取的大量隨機樣本的平均數的分布接近正態分布且平均數等于μ，標準差(也稱之為標準誤差)等于：

　　式中n——樣本單位數。

　　值得注意的是，中心極限定理的成立不考慮樣本總體的分布形狀，也就是說忽略了總體的分布類型，樣本平均數的分布會趨于正態分布。常用來表示總體分布、樣本分布和抽樣分布的平均數及標準差的符號都列在表5-2中。

　　表5.2 參數、統計量符號

　　平均數的標準誤差()之所以按前面所示的方法計算是因為，一個特定的樣本平均數分布的方差或是離差會隨著樣本數量的增加而減少。由常識可知，樣本數越大，單個樣本的平均數就越接近總體平均數。圖13-3表明了平均數的總體分布、樣本分布和抽樣分布之間的關系。我們將深入討論平均數的抽樣分布，而另一個比例抽樣分布，將在以后介紹。

　　5.5 平均數的抽樣分布

　　5.5.1 基本概念

　　考慮一個抽樣案例：一位調查人員以“在最近30天內至少吃過一次快餐的所有顧客”為總體，從中抽取了1000組容量為200的簡單隨機樣本。調查目的是要估計平均一個月內這些人吃快餐的平均次數。計算出每一組的平均數，按相關值確定區間，整理后便得到表中5-3的頻率分布圖。而圖5-4以直方圖的形式表示這些頻率，直主圖上方還可見到一條正態曲線。正如你所看見的，直方圖十分接近正態曲線的形狀。如果我們選取足夠的容量為200的樣本，計算每組的平均數，整理排列后所得的分布就是正態分布。圖5-4的正態曲線就是這項調查中平均數的抽樣分布。大樣本平均數的抽樣分布有以下特征：

　　(1)是正態分布

　　(2)分布的平均數等于總體平均數。

　　(3)分布有標準差，稱為平均數的標準誤差，它等于總體標準差除以樣本容量的平方根：

　　將標準差稱為平均數的標準誤差表明它更適用于樣本平均數的分布，而不是總體或樣本的標準差分布。記住這種計算只適合簡單隨機樣本，其他類型的樣本(如分層樣本和整群樣本)要用非常復雜的分式計算標準誤差。

　　表5.3 1000個樣本平均數的頻數分布

　　圖5.3 平均數的實際抽樣分布

　　5.5.2 根據單個樣本做出推斷

　　在實際操作中，人們往往不愿從總體中抽出所有可能的隨機樣本，畫出像表5.3和圖5.4那樣的頻率分布表和直方圖來。人們希望進行簡單的隨機抽樣，并據此對總體進行統計推斷。問題出現了，通過任一簡單的隨機樣本對總體均數進行的估計，其估計值在總體平均值±1個標準誤差內的概率究竟為多大?根據表5.2可知概率為68%，因為所有樣本平均數有68%都在此范圍內。而通過簡單隨機樣本對總體做的估計為實際總體平均值2倍標準誤差范圍內的概率為95%，在實際總體平均值3倍標準誤 差范圍內的概率為99.7%。

　　5.5.3點估計和區間估計

　　當利用抽樣要對總體平均值進行估計時，有兩種估計方法：點估計和區間估計。點估計是指把樣本平均值作為總體平均數的估計值。觀察圖5.3的平均數抽樣分布可知某一特定的抽樣結果，其平均數很可能相對更接近總體平均數。但是，樣本平均數分布中的任一個值都可能是這一特定樣本的平均值。有一小部分的樣本平均值與實際總體平均值有相當的差距，這種差距就叫抽樣誤差。

　　抽樣結果的點估計在很少的情況下完全準確，因此人們更偏于區間估計。區間估計就是對變量值如總體平均值的區間或范圍進行估計。除了要說明區間大小外，習慣上還要說明實際總體平均值在區間范圍以內的概率。這一概率通常被稱為置信系數或者置信度，區間則被稱為置信區間。

　　平均數的區間估計按以下步驟推導。從總體上抽出一定量的隨機樣本，計算出樣本平均數，可知這個樣本平均值存在于所有樣本平均數的抽樣分布中，但確切位置不清楚。此外還知道，這個樣本平均數在實際總體平均值±1個標準誤差范圍內的概率為68%，由此可知，實際值等于樣本值加上或減去1個標準誤差的信度為68%。用符號表示如下：

　　同理可知，實際值等于樣本估計值加上或減去2倍標準誤差(嚴格上是1.96，但為了計算簡單便通常用2)的置信度為95%，實際值等于樣本值加上或減去3倍標準誤差的置信度為99.7%。

　　以上都假設總體標準差已知，大多數時候，情況不是這樣。如果總體標準差已知，根據定義可以知道總體平均值，那就沒有必要事先抽取樣本了。而如果不知道總體標準差，那就必須通過樣本差去估計。

　　5.6 比例的抽樣分布

　　市場研究中經常會偏于進行比例或百分比方面的估計。下面是一些常見例子：

　　l 知道某一廣告的總體百分比;

　　l 平均一周上網1次以上的總體的百分比;

　　l 最近30天內吃過快餐和吃過4次以上快餐的總體百分比;

　　l 觀看某一電視節目的觀眾的總體百分比;

　　在上述情況下，總體比例或百分比是重要的因素，因此有必要介紹比例抽樣分布。

　　從特定總體中抽出大量隨機樣本，這些樣本的抽樣比例的相對頻率分布就是比例抽樣分布，它有以下特征：

　　Ø 近似于正態分布

　　Ø 所有樣本比例的平均值等于總體比例。

　　Ø 比例抽樣分布的標準誤差可以按下面的公式計算：

　　式中Sp—比例抽樣分票吳差;

　　P—總體比例的估計值;

　　n—樣本單位數。

　　考慮一下，如果需要估計一下最近90天內曾在網上購物的所有成年人的百分比，那么就像要得到平均數的抽樣分布一樣，要從成年人總體中選取1000組容量為200的隨機樣本，計算出1000組樣本中所有在最近90天內曾在網上購物的人數比例。這些值排列將形成一個趨于正態分布的頻率分布。這一分布的估計比例標準誤差可以用在前面計算比例標準誤差的公式來計算。

　　讀完下一節，你就會明白，市場人員對于樣本容量問題，更趨 于進行比例估計而不是平均值估計，是有其原因的。

　　5.7 樣本容量的確定

　　5.7.1平均值問題

　　考慮前面那個估計平均一個月快餐族吃快餐次數的案例，如果管理層需要對顧客的平均光顧次數做出估計，從而決定是否實行正在擬定的新促銷計劃。為了得到這個估計值，市場調研經理打算在總體中考察某個簡單隨機樣本。問題是，確定本次調查樣本容量的要素是什么?首先，對于估計平均值問題，計算所需的樣本容量的公式是：

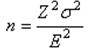
　　式中 Z―標準誤差的置信水平;

　　σ―總體標準差;

　　E―可接受的抽樣誤差范圍(允許誤差)

　　計算所需的樣本容量要有三種資料：

　　(1) 抽樣誤差的可接受的或允許的詳細范圍(E)。

　　(2) 標準誤差置信水平的允許確切值，也就是Z值。換一種說法，即總體平均值包括在指定置信區間內的置信度是多少?

　　(3) 最后需要估計一下總體標準差(σ)。

　　計算中要用到的置信水平(Z)和誤 差(E)必須由調查人員與他(她)的客戶進行磋商后才能確定。如前所述，置信水平與誤差范圍的確定不僅要根據統計原則，同時要顧及財務與管理方面的要求。理想的情況下，我們總是希望置信度很高，誤差很小。但要知道，這是經營決策，必須考慮成本問題。因此，要在精確度、置信度與成本之間進行權衡。有的時候，不要求很高的精確度與置信度。例如，你也許只想通過調查基本了解一下消費者對產品的普遍態度是正面有還是負面的。這里精確度就顯得不太重要了。但如果是一項產品創意測試，就需要精確度較高的銷售估計值，以便做出是否向市場推薦某種新產品的高成本、高風險的決策。

　　第三項是總體標準差的估計值，這是一個更麻煩的問題。我們在前面說過，如果總體標準差已知，那么也就能知道總體平均數(總體平均數是用來計算總體標準差的)。這樣的話就沒必要抽取樣本了。但調查人員如何不抽取樣本就估計出總體標準呢?結合使用以下四種方法可以解決這個問題：

　　(1) 利用以前的觀察結果。許多情況下，公司以前曾經進行過類似的調查，這時，可以利用以前的調查結果作為本次總體標準差的估計值。

　　(2) 進行試點調查。如果調查對象規模太大，可以投入一定的時間和資源對總體進行小規模的試驗調查。根據調查結果估計總體標準差確定樣本容量。

　　(3) 利用二手數據。有時候通過二手數據也可以對總體標準差做出估計。

　　(4) 通過判斷。如果其他方法都失敗了，還可以判斷總體標準差。即把許多管理人員的判斷集中起來進行分析，而這些管理人員都有能力對有關的總體參數做出有所根據的猜測。

　　當完成了調查，計算出樣本平均值和樣本標準差后，調查人員就可以正確估計出總體標準差，并確定所需的樣本容量了。這時如果需要，可以對以前的抽樣誤差估計做出調查。

　　再來考慮估計快餐族平均每月吃快餐的平均次數。以下這些值將代入下面的公式。

　　l與公司的管理者進行磋商后，市場調研經理認為有必要估計一下吃快餐的平均次數。考慮到管理者對精確度的要求，她規定估計值不得超過實際的0.10(1/10)。這個值(0.01)將作為E值代入公式。

　　l此外，市場調研經理還認為，考慮全局，需要把實際總體平均值在(樣本平均值±E)區間以內的置信度定為95%。而若要置信度為95%，就必須在2倍標準誤差范圍內(嚴格是1.96)。因此，2作為Z值代入公式。

　　l最后，確定公式中的值。幸好公司一年前曾做過類似的調查。調查對象是最近30天內吃快餐的平均次數。其標準差是1.39，以此作為s值最好不過。因此把1.3代入公式。然后進行計算，通過計算，可知樣本容量為772時可以滿足提出的要求。

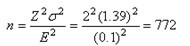
　　5.7.2計算比例的問題

　　考慮估計最近90天內曾在網上購物的所有成年人的比例或百分比的案例。其目標是從成年人總體中抽取一個簡單隨機樣本，估計其比例是多少。下面討論一下如何確定代入公式的那幾個值：

　　l 像前面說的，要根據抽樣結果估計總體平均值，首先要確定E的值。例如，假設可接受的誤差范圍為±2%，那么將0.02作為E的值代入公式。

　　l 其次，假設調查人員要求抽樣估計在實際總體比例的2%范圍以內的置信度為95%，那么按前面講的，把2作為值代入公式。

　　l 最后一點，在一年前的一次類似調查中，有5%的被調查者表示在最近90天內曾在網上購物。我們可以用0.05作為P值代入公式。

　　計算過程如下：

　　根據要求，需要一個475個人的隨機樣本。要注意的是，與確定估計平均值所需的樣本容量的過程相比，調查人員在確定估計比例所需的樣本容量時有一個優勢：如果缺乏估計P的依據，可以對P值做最悲觀或最糟糕的假設。給定Z值和E值，P值為多大時要求的樣本量最大呢?當P=0.5時，“P(1-P)”有極大值0.25存在，如此設定P值樣本是最大。而給定Z值和E值，對于與平均估計所需樣本量有關的值就沒有最悲觀的假設。

　　5.7.3總體容量樣本容量

　　你也許會注意到計算樣本容量的公式中沒有一個用到總體容量。學生們(和經理們)經常會注意到這個問題。表面上看來好像是要抽取的樣本量越大，其總體容量也應該增大。其實不然。通常，總體容量與在一定誤差和可靠度范圍內估計總體參數所需的樣本容量之間沒有直接的關系。實際上，總體容量只有當樣本容量相對它而言過大時才會起作用。根據經驗，當樣本容量超過總體的5%時，就需要調整樣本容量了。一般都假設樣本的抽取是相互獨立的(獨立假設)，這一假設在樣本相對于總體很小時成立。當樣本量占總體比例相對較大(5%以上)時就不成立了。因此， 們必須調 整一下標準公式。譬如，前面的計算平均數標準誤差的公式是：

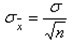
　　當樣本量占總體5%以上，就要推翻獨立假設。調整后的正確公式是：

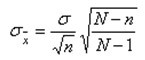
　　其中，(N-n)/(N-1)被稱為有限總體修正系數(FPC)。當樣本占總體的5%以上，調查人員可以通過FPC來減少所需的樣本容量。計算公式如下：

　　式中，n’為修改后的樣本量;n為原樣本量;N為總量。

　　如果總量為2000，原樣本量為400，則：

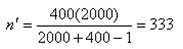
　　經過FPC的調整，需要的樣本量由原先的400變成了333。

　　問題關鍵不是樣本量大小與總量大小的關系，而是選取的樣本是否能真實代表總體的特性。經驗表明，經過仔細挑選的樣本，盡管容量不大，卻也能十分準確地反映總體特征。許多著名的全國性調查和民意測驗的樣本數都不超過2000。蓋洛普民意測驗、哈里斯民意測驗和尼爾森電視節目受歡迎程度調查都是很好的例子。這些例子都表明，即使調查對象是數千萬人的行為，也可以通過對于總體相當小的一部分樣本進行十分準確的預測。

　　5.7.4確定分層樣本和整體樣本的容量

　　本章列出的計算樣本容量的公式只適用于簡單隨機樣本。當然也有適用于其他如分層樣本、整群樣本確定樣本容量和抽樣誤差范圍的公式。雖然本章提到的許多概念對這些樣本都適用，但它們的計算公式卻要復雜很多。而且，公式中要用到的數據往往很難得到。因此，這些樣本的容量確定問題超過了本書的介紹范圍。有興趣的讀者可以參考高級教材。

　　5.8統計權

　　盡管在市場調研中用本章節公式計算樣本量是十分標準的作法，但這些公式都只承認第一類誤差(不存在差值時推斷差值存在而產生的誤差)。它們顯然不考慮第二類誤差，即實際存在差值時認為沒有差值而產生的誤差。不發生第二類誤差的概率叫統計權。計算樣本容量的標準公式默認統計權為50%。舉個例子，如果要確定兩種產品中哪一個對目標顧客群更有吸引力，并且可能進行購買的目標顧客的百分比之間可以有5%的差值，這時標準樣本容量公式要求每項產品需要的樣本容量大約為400。通過這一計算，我們默認了一個事實，即有50%的可能我們會錯誤地推斷出兩種產品具有相等的吸引力。

　　參考文獻：

　　1 《當代市場調研》 Carl McDaniel,Jr and Roger Gates 著，范秀成等譯 機械工業出版社出版 2001

　　2 《實用統計分析方法》 蔣慶瑯著，方積乾等譯 北京大學、中國協和醫科大學聯合出版社出版 1998

　　3 《社會統計分析方法》 郭志剛主編 中國人民大學出版社出版 1999

上一篇下一篇