欧美性欲视频_国产一区正在_91久久精品国产91性色tv_精品动漫3D一区二区三区免费版_91精品久久久久久久_久久天天操

　　本章主要內容：

　　l 計量資料的統計描述，主要包括資料的位置指標與離散指標

　　l 計數資料的統計描述，主要包括率、構成比、相對比等

　　2.1 計量資料的統計描述

　　2.1.1 頻數表(frequency table)

　　2.1.1.1 頻數表的概念及制作

　　制作頻數表是整理計量資料最常用的方法，現以實例介紹頻數表的制作方法。

　　例2.1 1999年，某飲料公司以街訪的方式對100名消費者進行了500ml瓶裝可樂的價格進行了測試，關于問題‘您認為最合適的價格應該是多少?’的回答，資料如下(單位：元)：

 

　　(1) 尋找資料中的最大值、最小值，計算極差

　　本例最大值M=3.22

　　最小值m=1.71

　　最大值與最小值之差稱為極差，常用R表示

　　R=M-m=3.22-1.71=1.51

　　(2) 確定組距、組段數

　　頻數表一般設10~15個組段，觀察值少時可相對少些，組段數n多時可多些，

　　組段數為n，組距h，極差R有如下關系：

　　本例共100個數據，可分10個組段，n=10，則h=1.51/10=0.151»0.15

　　各個組段應界限分明，每個組段的起點稱為‘下限’(low limit)，終點稱為‘上限’(upper limit)，各個組段從本組段的‘下限’開始，不包括本組段的‘上限’;第一組應包含資料中的最小觀測值，最后一組應包含資料中的最大值;第一組從最小值開始，或一個符合日常習慣的數值開始，如，本例可從1.70開始，第一組段為1.70~，第二組段為：1.85~，依次類推，最后一個組段為，見表2.1第一列

　　(3) 掃描樣本值，劃計后獲得頻數

　　劃記的方法是，按行(或者按列)，從第一個原始數據開始，逐一判斷該數據屬于哪一個組段，然后在相應的組段作一個記號，本書采用‘*’作為記號。如：第一個數據‘2.67’，屬于第七個組段‘2.60~’，在相應組段劃‘*’，第二個數據2.88，屬于第八個組段‘2.75’，在相應組段‘2.75~’作記號‘*’，依次類推，直至將所有的數據‘讀完’，得到表2.1的第二列，劃記完成，清點第二列每組段的‘*’數，得到相應組段的頻數，記入第三列，第一、第三列即為做的頻數表。

　　表2.1 100名被訪者關于500ml可樂認可價格的頻數表

　　從頻數表的制作過程可見，頻數表是反映原始數據在每一個組段數據出現頻次的表格。

　　2.1.1.2 頻數表的用途

　　(1) 從表2.1可見，數據向組段‘2.45~’集中，以該組段周圍的原始數據居多，原始資料向某一數據段(或某一數據)周圍的集中、靠攏的特點，在統計學上稱為資料的集中趨勢。

　　(2) 從表2.1還可看到，原始數據有大有小，差異較大，最大值與最小值相差1.51，從1.71到3.22，從中央向兩側逐漸減少，而這種從小到大的分布特點，在統計學上稱為離散趨勢。

　　(3) 從表2.1還可看到，第一組段有2個數據，最后一個組段有1個數據，最小、與最大清楚地擺在面前，有利于我們去重點監督。

　　由此可見，頻數表至少有如下用途：

　　1)揭示資料的分布特征和分布類型

　　2)便于發現某些特大、特小的可疑值

　　3)便于指標計算和統計分析

　　2.1.1.3 頻數分布的常見類型

　　(1) 對稱分布 表2.1是頻數表最常見的類型，資料集中在某一數據的周圍，左右兩側對稱，資料的這種分布，稱為對稱分布。

　　(2) 偏態分布 表2.2，資料偏向價格較大的一側，表2.3，資料偏向價格較小的一側，資料的這種分布稱為偏態分布。其中，向大的一側偏向，稱為正偏態分布;向小的一側偏向，稱為負偏態分布。

　　表2.2 某資料的頻數表

　　表2.3 某資料的頻數表

　　2.1.2 資料的集中趨勢

　　平均數(average)：統計應用中最重要的一個指標體系，常用于描述一組變量值的集中位置，代表平均水平。或者說它是集中位置的特征值。

　　平均數的計算和應用要求資料必須具備同質的基礎，否則，計算的指標沒有實際意義，如：把電視價格與冰箱的價格放在一起相加，沒有任何意義。

　　常用的平均數包括：均數、幾何均數、中位數、眾數等，下面一一介紹。

　　2.1.2.1 均數(mean)

　　均數是算術平均數的簡稱，其計算是將觀測值相加，然后除以資料的個數，是最常用的平均數的計算方法，反映一組觀測值在數量上的平均水平。

　　(1) 計算公式

　　假定觀測值為x1、x2、 … xn，公式為

                                                             　(2.1)

　　如：5家商店21英寸的彩電的銷售價格分別為：1038、995、1120、1080、1088，則五家商店的平均價格(均數)為

　　由于公式(2.1)按照算術平均數的定義直接計算，公式所表達的含義也比較清楚，故稱之為直接法。當資料中相同的觀測值較多時，可將相同觀測值的個數，即頻數f，乘以該觀測值X，以代替該觀測值逐個相加，如：資料中有5家商店價格均為1088，則在計算時，不必：1088+1088+1088+1088+1088=5440，而直接用5乘1088即可：1088´5=5440，頻數5在統計學上也稱為權重，由此得到計算均數的‘加權法’公式：

                                                                      (2.2)

　　例：見表2.1，計算100名消費者對500ml瓶裝可樂的平均價格

　　計算表2.1中每組的組中值，計算方法是：將每組的上限與下限相加，然后除以2，如：第一組，下限為1.70，上限為1.85，組中值為(1.70+1.85)/2=1.775，結果見表中第三列。組中值是屬于該組段的原始數據的代表，如，第一組段有2個數據，我們可以認為，這兩個觀測數據均為1.775，然后計算每一組段的觀測數據的代數和，即組中值乘以相應頻數，得第四列數據，將第四列相加，得所有觀測值的代數和，由公式(2.2)計算出均數為：2.50(元)

　　表2.4 100名消費者對500ml瓶裝可樂的平均認可價格的計算

　　均數的兩個重要特性：

　　各離均差的代數和等于0，即

 

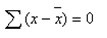
　　離均差為每個觀測值與均數的差值，即： ，反映每一個個體觀測值相對與均數的離散情況。如：第一家商店彩電價格為1038元，相對與平均價格1064.2元，離均差為：1038-1064.2= -26.2，既，第一家商店比平均價格低26.2元。

　　(2)離均差的平方和小于各觀測值與任何數之差的平方和。

　　應用范圍：均數反映全部觀測值的平均水平，因而應用非常廣泛。但它最適用于對稱分布資料，尤其正態分布資料。

　　2.1.2.2 幾何均數(geometric)

　　計算方法：

　

　　(1)直接法：

　　(2)加權法：

　　2.1.2.3 中位數(median)

　　將一組觀察值按從小到大順序排列，位次居中的觀察值稱為中位數。全部觀察值中，大于和小于中位數的觀察值個數相等，常用M表示。

　　計算公式：資料按從小到大的順序排序x1£x2£ … £xn

　　當n為奇數時，

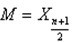
　　當n為偶數時，

　　如：調查了5家工廠的職工數，分別為：15，30，61，180，500，中位數M=61人;若調查了6家，分別為：15，30，61，100，180，500，則中位數M=(61+100)/2=80.5(人)

　　2.1.2.4 眾數(mode)

　　全部觀察值中，出現頻率最多的那個觀察值稱為眾數。

　　在推出400ml洗發水前，某企業舉行了一場有關其價格定位的座談會，8位專家中有5位認為該產品定價應為35元，則8個調查數據中35出現的頻次最高，因此其眾數為：35元。

　　2.1.2.5 百分位數(percentile)

　　百分位數是位置指標，以Px表示。Px將總體分成兩部分，理論上有x%的觀察值比它小，(100-x)%的觀察值比它大，中位數是特殊的百分位數。

　　利用頻數表計算百分位數的公式為：

　　式中fx為Px所在組段的頻數，i為該組段的組距，L為其下限，SfL為小于L的個組段的累計頻數。

　　例，某資料的頻數分布見表2.5，首先計算頻率，樣本含量為114，每一組段的頻數除以樣本含量得該組段的頻率，見第三列，每一組段的頻數加上前面各組段的頻數，得該組段的累計頻數，見第四列。

　　(1) 計算百分之25位數P25，從表2.5第五列可見，從第一組段至第二組段，即從1.70至2.00(不包括2.00)，共含有樣本總數21.93%的個體，從第一組至第三組，共含有總數38.6%的個體，根據百分位數的定義，P25應在第三組段的范圍內，因此，L=2.00，i=0.15，fx=19，SfL=21.93 又n=114，x%=25%

　　由公式，

　　同理，可計算P50，即中位數M及P75

　　表2.5 百分位數的計算

　　2.1.3 離散趨勢

　　2.1.3.1 極差(range，簡記為R)

　　一組資料中，最大值與最小值之差稱為極差，常用R表示。用M表示最大值，m表示最小值，計算公式為：

　　R=M-m

　　如：某資料，最大值M=3.22，最小值m=1.71，則極差R=3.22 - 1.71=1.51

　　優點：利用極差來說明資料變異度的大小，簡單明了，在資料描述時經常用到。

　　缺點：除最大、最小值外，不能反映其它數據的變異情況;不夠穩定，當樣本量相差懸殊時，不宜進行樣本間變異度的比較。

　　2.1.3.2 四分位數間距(quartile,Q)

　　P25位數，表示全部觀測值中，四分之一的觀測值比它小;P75，表示四分之一的觀測值比它大，因而稱P25、P75為四分位數，其中P25為下四分位數，常用QL表示，P75為上百分位數，常用QU表示

　　Q=QU-QL=P75 - P25

　　如：前面的例題中，QL P25=2.03，QU =P75=2.40，則：

　　Q=QU-QL=2.40-2.03=1.3

　　優點、缺點同極差類似，四分位數間距比極差穩定。

　　2.1.3.3 方差(variance)

　　用極差或四分位數間距來描述資料的變異情況，僅用到資料中的兩個數據，不能反映其他資料的情況，為反映資料中的所有個體對變異度的影響，研究中首先想到了離均差這一指標。以均數為m的總體為例，離均差之和即S(x-m)=0，自然想到將每一個觀測值的離均差平方后再相加(稱為離均差平方和，英文：sum of squares，簡記為SS或lxx)，即計算S(x-m)2，由于其大小還與個體的數目有關，故將其除以變量值的個數N后，得到描述總體變異的指標---方差，公式為：

                               　(2.09)

　　公式(2.09)稱為總體方差，對樣本而言，數理統計證明，方差為：

                                          　(2.10)

　　加權公式為：

                                    　(2.11)

　　公式(2.10)稱為樣本方差，其中n-1稱為自由度(degree of freedom)。

　　例，計算例2.1資料的標準差

　　由表2.1，åfx=250.85，åfx2=640.19 n=åf=100，代入公式(2.11)

　　關于方差的分子部分，即離均差平方和，還可以寫成如下表達式：

            　(2.12)

　　2.1.3.4 標準差(standard deviation)

　　方差的單位是原單位的平方，將之開方后，即得常用于描述資料變異度的指標—標準差，總體標準差用s，樣本用S表示，計算公式分別為

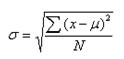                        　(2.13)

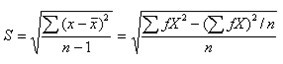                       　(2.14)

　　例2.1資料的標準差S為

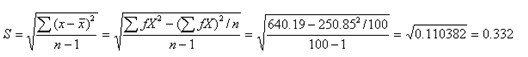
　　2.1.3.5 變異系數(coefficient of variation， 簡記為CV)

　　變異系數亦稱離散系數(coefficient of dispersion)，計算方法是將標準差S與均數 的比值，公式為：

　　應用：(1)度量衡不同的資料間變異度的比較

　　(2)均數相差懸殊的資料間的比較

　　2.2 分類資料的統計描述

　　2.2.1 常用相對數

　　2.2.1.1 率(rate)

　　率，又稱頻率指標，它說明某現象發生的頻率或強度。

　　如：調查了100間零售店，其中35間有某產品出售，則該產品的鋪貨率為：

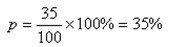
　　在有關洋酒的調查中，100名被訪者中有85人知道馬爹利，則馬爹利的知名度為：

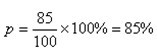
　　2.2.1.2 構成比(proportion)

　　構成比又稱構成指標，它說明一事物內部各組成

　　部分所占的比重或分布，常以百分數表示。

　　如：調查了100名被訪者，其中大專及以上學歷者55人，則100名被訪者中，大專及以上學歷人員占的比例為：

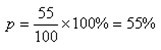
　　2.2.1.3 相對比(ratio)

　　相對比簡稱比，是兩個相關指標之比，說明兩個指標的相對水平。計算公式為：

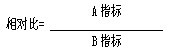
　　例：某品牌，在上海的知名度P1=0.65，在廣州為P2=0.38，則該品牌的知名度上海相對與廣州的相對比為：

　　廣州相對與上海的相對比為：

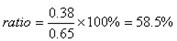
　　2.2.2 顧客滿意表征指標(舉例)

　　2.2.2.1 知曉度

　　知曉度=知曉人數/目標公眾

　　2.2.2.2 知名度

　　(1)絕對知名度=認為企業或產品有名氣的人數/目標公眾

　　(2)相對知名度=認為企業或產品有名氣的人數/知曉人數

　　2.2.2.3 美譽度

　　(1)絕對美譽度=褒揚者人數/目標公眾

　　(2)相對美譽度=揚者人數/知曉人數

　　2.2.2.4 指名度

　　(1)絕對指名度=指名消費人數/目標公眾

　　(2)相對指名度=指名消費人數/知曉人數

　　2.2.2.5 滿意度

　　(1)絕對滿意度=滿意人數/目標公眾

　　(2)相對滿意度=滿意人數/消費人數

　　2.2.3 動態數列及其分析指標

　　動態數列(dynamic series)是一系列按時間順序排列起來的統計指標，包括絕對數、相對數或平均數，用以說明事物在時間上的變化和發展趨勢。

　　現以實例介紹常用指標及其計算。

　　例，表3.1第(2)列給出了某公司1996~2000年凈資產資料，現分析該公司該公司凈資產逐年變化特點。

　　表3.1 某公司1996~2000年凈資產資料分析表

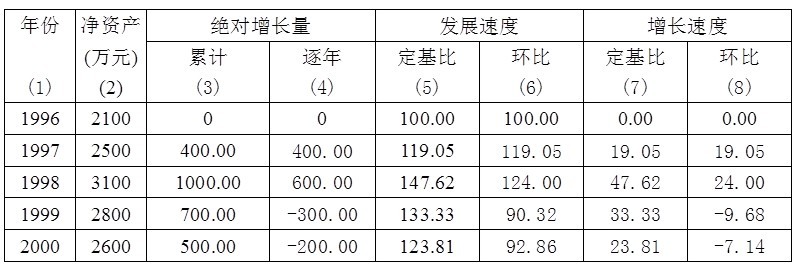
　　2.2.3.1 絕對增長量 說明事物在一定時期所增加的絕對的數量。絕對增長量常計算累計增長量、逐年增長量

　　(1) 累計增長量 以某年作為比較對象(基期)，其它年份與其相減，所得差值即為累計增長量。

　　本例以1996年數據作為基數，如：1998年凈資產累計增長量為：2500-2100=400(萬元)，其余年份的累計增長量見表3.1第(3)列。

　　(2) 逐年增長量 以下一年的數據與上一年的數據相減，所得差值即為逐年增長量。

　　本例以1997年凈資產為2500萬元，1998年為3100萬元，1998年相對于1997年增長量為：3100-2500=600(萬元)，其余年份的逐年增長量見表3.1第(4)列。

　　2.2.3.2 發展速度和增長速度

　　發展速度和增長速度常計算的指標是定基比、環比，增長速度=發展速度-1。

　　(1) 定基比，針對某一時間序列，統一用某個時間的指標作基數，以各時間的指標與之相比。反映變化的發展趨勢。

　　如：以1996年凈資產2100萬元作為基數，1998年為3100萬元，1998年相對于1996年的發展速度(定基比)為：

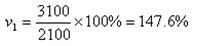
　　1998年對1996年增長速度(定基比)為：

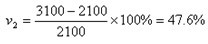
　　增長速度亦可由發展速度計算：

　　

　　其他時期的定基比見表3.1第(5)、(7)列。

　　(2) 環比，針對某一時間序列，以前一個時間的指標作基數，以相鄰

　　的后一時間的指標與之相比。反映年度間的波動。

　　如：以1997年凈資產2500萬元作為基數，1998年為3100萬元，1998年的環比發展速度為：

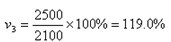
　　1998年的環比年增長速度為：

　　增長速度亦可由發展速度計算：

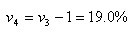
　　其他時期的環比指標見表3.1第(6)、(8)列。

　　2.2.3.3 平均發展速度/增長速度

　　平均發展速度/增長速度用于概括某一時期的速度的變化，計算公式如下：

　　假定基期數據為a0,各時期數據如下：a0、a1、a2、a3、…、an，an為第n的指標數據，則

　　平均發展速度

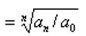
　　平均增長速度=平均發展速度-1

　　如：以1996年為基期，1999年凈資產為2800萬元，則a0=2100，n=3,a3=2800, 平均發展速度為：

　　平均增長速度=平均發展速度-1=110.1%-1=10.1%

　　自1996年至1999年，凈資產平均發展速度為110.1%，平均增長速度為10.1%。

上一篇下一篇